目录
其他材料
距离——勾股定理，length()函数
我们有不同的理由需要测量两点之间的距离——例如，书写一个跨度计算脚本或创建邻近效应。正如我们前面讨论的，要计算两点之间线段的距离，我们只需对两点的对应的矢量进行减法运算，运算后所得到的矢量的长度就是两点之间的距离。
在AE中，有两种计算矢量长度的方法，一种是复杂方法，另外一种是简单方法。首先让我们了解一下复杂方法：
勾股定理
还记得我们中学几何中学习的勾股定理吧，在该定理中规定了，直角三角形中斜边的平方等于两个直角边的平方和:
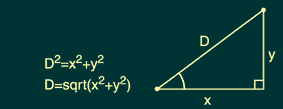
在前面的教程中我们提到过，任何一个二维矢量都可以组成一个直角三角形，所以我们可以使用勾股定理来计算任意两点之间的线段长度。首先我们通过计算来找到表示两点之间线段的矢量，然后将它分离出来，最后使用勾股定理就可以计算出这条线段的长度。
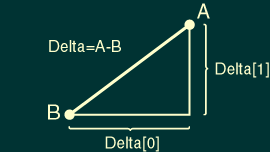
根据Javascript语法对表达式的规定，我们需要书写下面的表达式来完成上面的计算过程：
// 拾取两点
point1=this_comp.layer("A").position;
point2=this_comp.layer("B").position;
// 计算出两点之间的矢量
delta=sub(point1, point2);
X=delta[0];
Y=delta[1];
// 计算矢量长度
distance=Math.sqrt(X*X+Y*Y);
不是很复杂是么，但是还有一个更简单的方法。
length(vector)
在AE表示式中内置了一个函数来计算矢量的长度：length()函数。将该函数应用到任何维数的矢量中就会返回矢量的长度，
使用length()函数，我们可以重新书写上面的表达式：
// 拾取图层
point1=this_comp.layer("A").position;
point2=this_comp.layer("B").position;
// 计算出两点之间的矢量
delta=sub(point1, point2);
// 计算矢量长度
length(delta);
使用这种方法不仅书写简便而且理解记忆起来要比使用勾股定理要简便得多。这种方法还有一个优点就是可以计算出任何维数矢量的长度，我们也可以将勾股定理应用到三维图矢量中，但是非常麻烦。
实例应用：交互模糊
说了这么多，这种计算方法究竟可以应用到什么地方呢？一个最明显的应用就是应用这种方法来控制图层或者是效果参数。在下面的例子中，
我们将使用前面提到过的插值算法首先将距离值范围重新设定以影响快速模糊效果，然后再设定该距离范围以影响缩放参数。
在第一个合成中，我们分别对四个图层应用了快速模糊效果并为它们的模糊程度属性加入了相似的表达式，同时使用一个名为"Drag Me"的黄色固态层来控制受控图层的模糊程度。在表达式中我们使用了liner()插值算法将位移的范围从0至80缩减到40至0，所以当控制图层接近受控图层时，模糊效果将会变得更加强烈。
完成上面的设置后，我们就可以通过调整控制图层的位置来依次交互的影响四个受控图层，在渲染前，将控制图层的显示开关关掉，这样我们就可以完成整个动画了。
下面就是完整的表达式：
// 为受控图层加入快速模糊效果
// 为模糊程度加入表达式
// Point1 是当前受控图层的位置, point2 是控制图层的位置
point1=this_layer.position;
point2=this_comp.layer("Drag Me").position;
// 计算出两点之间的矢量线段
delta=sub(point1, point2);
// 计算出该矢量的长度
distance=length(delta);
//使用 linear() 的方法将 distance 的范围重新设定为40至0
linear(distance, 0, 80, 40, 0);
实例应用：缩放
在第二个合成中，我们将类似的表达式应用在了受控图层的缩放属性上，创建一个动态缩放的效果：
在这里表达式的书写基本上与前一个合成中的相同，因为缩放属性是一个二维数组（如果转化为3D图层就是三维数组），我们只需要将最后一句重新调整一下就可以了， (要详细了解矢量与数组单击这里)
//重新设定距离范围，以使图层越接近时缩放值越大，图层距离越远时，缩放值越小
linear(distance, 0, 80, [250,250], [75,75]);